Devoir Maison
D'après Bac ES Liban 2008
Soit \(f\) une fonction définie et dérivable sur l'intervalle \([−4 ; 6]\).
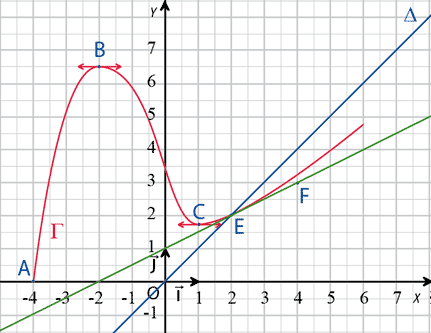
On note \(f'\) sa fonction dérivée. La courbe \(\Gamma\) représentative de la fonction \(f\) dans un repère orthonormal est tracée ci-dessous ainsi que la droite \(\Delta\) d'équation \(y=x\).
La courbe \(\Gamma\) et la droite \(\Delta\) se coupent au point \(E\) d'abscisse \(2\).
On sait par ailleurs que :
- la courbe \(\Gamma\) admet des tangentes parallèles à l'axe des abscisses aux points \(B (−2 ; 6,5)\) et \(C (1 ; 1,75)\)
- la droite \((EF)\) est la tangente à la courbe \(\Gamma\) au point \(E\)
- \(F\) est le point de coordonnées \((4 ; 3)\)
1
Dans cette question, déterminer par lecture graphique et sans justification :
a
les valeurs de \(f' (−2)\) et \(f' (2)\)
b
les valeurs de \(x\) dans l'intervalle \([−4 ; 6]\) vérifiant \(f'(x)\geq 0\) ;
c
les valeurs de \(x\) dans l'intervalle \([−4 ; 6]\) vérifiant \(f (x) \leq x\).
2
Encadrement d'une intégrale
Dans cette question, toute trace de recherche, même incomplète, ou d'initiative non fructueuse sera prise en compte dans l'évaluation.
a
Soit l'intégrale \(I= \int_2^3{f (x) dx}\). Interpréter graphiquement \(I\).
b
Proposer un encadrement de l'intégrale \(I\) par deux nombres entiers consécutifs. Justifier.